Fair Coins

I’m starting to read a book called Probabilistic Programming and Bayesian Methods for Hackers by Cameron Davidson-Pilon, who is the Data lead at Shopify. You can download it for free; each chapter is an IPython notebook. I’ve read the first four chapters so far and have really enjoyed them. This book is perfect for people like me who have a foundational understanding of Bayesian methods as well as comfort coding in Python (specifically, using the data stack). I like how he writes very concisely, and provides original examples.

In Chapter 1, the first example given is the famous “Given x tails and y tosses, is the coin fair or not”. I’m familiar with the frequentist approach, which is to model the coin flip as a random Binomial variable ~ B(y, 0.5) and determine the probability of getting a result as extreme as x. When y is large, the distribution converges to Normal. Here is the R code:

passum = 0.5
# by proportion
proptest = function(tailnum, tosses) {
	phat = tailnum/tosses
	stdev = sqrt(passum*(1-passum)/tosses)
	zscore = (phat-passum)/stdev 
	round(1-pnorm(zscore),4)
}  
# by count
freqtest = function(tailnum, tosses) {
	phat = tailnum/tosses
	stdev = sqrt((passum*(1-passum))*tosses)
	zscore = (tailnum - passum*tosses)/stdev
	round(1-pnorm(zscore),4)
}
# or simply
simpleway = function(tailnum, tosses) {
	1-pbinom(tailnum, tosses, passum)	
}

So, for example, the chances of getting 550 or more tails in 1000 tosses with a fair coin is about 8 × 10^-4. However, with smaller sample sizes (i.e., tosses), it is not always accurate to make the normality assumption.

This is when the Bayesian approach comes in handy. Like before, we can model the flips as a Binomial variable (or, multiple Bernoulli variables).The conjugate prior for the Binomial is the Beta distribution. Basically, what this means is that if the likelihood function is Binomial and the prior function is Beta, then the posterior will also be a Beta function.

The following is an example of how the curves shift as the sample size grows. I adapted this from the Python version in the PPBMH book.

set.seed(2015-09-04)
n_trials = c(0,1,2,3,4,5,8,15,50,500)
data = rbinom(tail(n_trials,1), 1, 0.5) # 0 tails, 1 heads
x = seq(0,1,length=100)
plotme = function(N, dat=data) {
    if(N==0) { 
        heads = 0 
        tails = 0
    } else { 
        heads = sum(dat[1:N])
        tails = N-heads
    }
    y = dbeta(x, 1+heads, 1+tails)

    plot(x, y, type="l", xlab=expression(paste(bolditalic(p), ", probability of heads")), yaxt="n", ylab="", col="#E66700", lwd=4)
    if(N==0) rect(min(x), 0, max(x), max(y), col="#FF9C4D", border=NA)
    else polygon(c(0, x, max(x)), c(0, y, min(y)), col="#FF9C4D", border=NA)
    abline(v=0.5, col="black", lty=2)
    legend("topright", legend=paste("observe", heads, "heads and", tails, "tails"), fill="#FF9C4D", cex=0.75)
}
invisible(lapply(n_trials, plotme))

As shown, the probability distribution goes from Uniform to one that resembles the standard Gaussian as more evidence is provided, since the evidence was taken from a distribution corresponding to a fair coin. So, if the coin were biased, then we expect the posterior distribution to look more skewed towards the true (biased) mean.

With small samples, the results might seem biased even if the coin is actually fair. In these situations, it’s much more intuitive to think of the real distribution transforming as more information is provided. For example, if we flip the coin 10 times and see 7 heads and 3 tails, here is what the distribution would look like:

data3 = c(0,0,0,1,1,1,1,1,1,1) # order doesn't matter 
plotme(10, data3)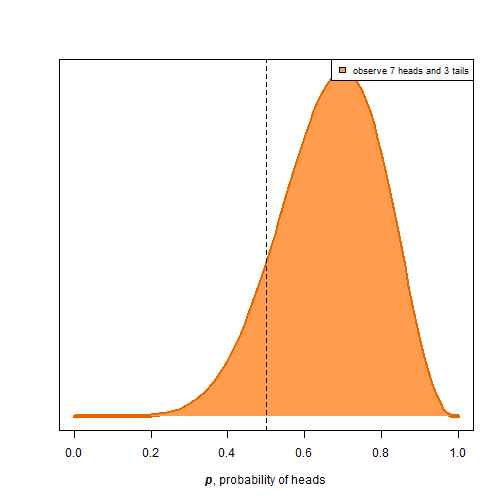

Most of the area is in the 0.65-0.75 region rather than the 0.45-0.55, so given the result, this coin is more likely to be biased than fair. However, it’s probably more Bayesian to say that there is a 13.02% chance that a coin is fair given the observations. This is much more interpretable than conducting a hypothesis test and concluding that, “if the coin were fair, there is a z chance to observe a result as extreme”.

Back to reading! And again, you can (and absolutely should) download the book for free here. I can already tell it’s going to be a good one!

If you have any feedback or questions for me, please shoot me an email at melodyyin@u.northwestern.edu. Thank you!